14 KiB
14 KiB
title, subtitle, author, affiliation
| title | subtitle | author | affiliation |
|---|---|---|---|
| Evaluation of the Performance of Randomized FFD Control Grids | Master Thesis | Stefan Dresselhaus | Graphics & Geometry Group |
Motivation
- Evolutionary algorithms cope especially well with these problem domains
- But formulation can be tricky
Motivation
- Problems tend to be very complex
- i.e. a surface with
nvertices has3\cdot nDegrees of Freedom (DoF).
- i.e. a surface with
- Need for a small-dimensional representation that manipulates the high-dimensional problem-space.
- We concentrate on smooth deformations ($C^3$-continuous)
- But what representation is good?
What representation is good?
- In biological evolution this measure is called evolvability.
- no consensus on definition
- meaning varies from context to context
- measurable?
- Measure depends on representation as well.
RBF and FFD
- Andreas Richter uses Radial Basis Functions (RBF) to smoothly deform meshes
RBF and FFD
- My master thesis transferred his idea to Freeform-Deformation (FFD)
- same setup
- same measurements
- same results?
Outline
- What is FFD?
- What is evolutionary optimization?
- How to measure evolvability?
- Scenarios
- Results
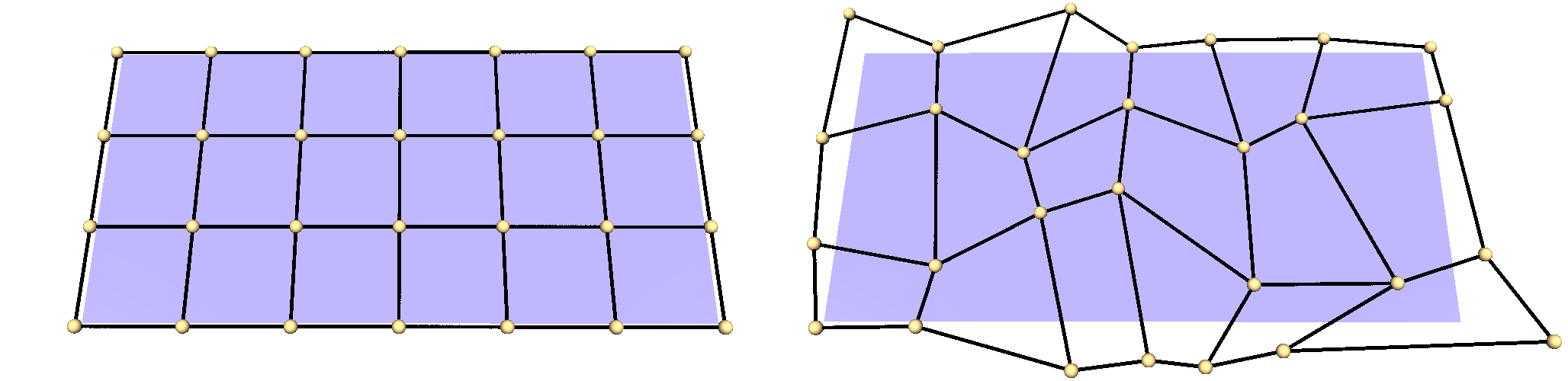
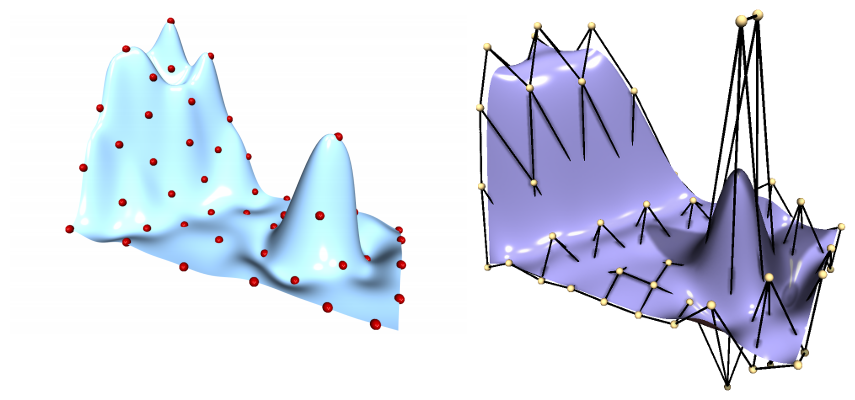
What is FFD?
- Create a function
s : [0,1[^d \mapsto \mathbb{R}^dthat is parametrized by some special control--pointsp_iwith coefficient functionsa_i(u):s(\vec{u}) = \sum_i a_i(\vec{u}) \vec{p_i} - All points inside the convex hull of
\vec{p_i}accessed by the rightu \in [0,1[^d.
Definition B-Splines
- The coefficient functions
a_i(u)ins(\vec{u}) = \sum_i a_i(\vec{u}) \vec{p_i}are different for each control-point - Given a degree
dand position\tau_ifor the $i$th control-pointp_iwe define \begin{equation} N_{i,0,\tau}(u) = \begin{cases} 1, & u \in [\tau_i, \tau_{i+1}[ \ 0, & \mbox{otherwise} \end{cases} \end{equation} and \begin{equation} \label{eqn:ffd1d2} N_{i,d,\tau}(u) = \frac{u-\tau_i}{\tau_{i+d}} N_{i,d-1,\tau}(u) + \frac{\tau_{i+d+1} - u}{\tau_{i+d+1}-\tau_{i+1}} N_{i+1,d-1,\tau}(u) \end{equation} - The derivatives of these coefficients are also easy to compute:
\frac{\partial}{\partial u} N_{i,d,r}(u) = \frac{d}{\tau_{i+d} - \tau_i} N_{i,d-1,\tau}(u) - \frac{d}{\tau_{i+d+1} - \tau_{i+1}} N_{i+1,d-1,\tau}(u)
Properties of B-Splines
- Coefficients vanish after
ddifferentiations - Coefficients are continuous with respect to
u - A change in prototypes only deforms the mapping locally
(betweenp_itop_{i+d+1})
Definition FFD
- FFD is a space-deformation resulting based on the underlying B-Splines
- Coefficients of space-mapping
s(u) = \sum_j a_j(u) p_jfor an initial vertexv_iare constant - Set
u_{i,j}~:=~N_{j,d,\tau}for eachv_iandp_jto get the projection:
or written with matrices:v_i = \sum_j u_{i,j} \cdot p_j = \vec{u}_i^{T} \vec{p}\vec{v} = \vec{U} \vec{p} \vec{U}is called deformation matrix
Implementation of FFD
- As we deal with 3D-Models we have to extend the introduced 1D-version
- We get one parameter for each dimension:
u,v,winstead ofu - Task: Find correct
u,v,wfor each vertex in our model- We used a gradient-descent (via the gauss-newton algorithm)
Implementation of FFD
- Given
n,m,ocontrol-points in $x,y,z$--direction each Point inside the convex hull is defined byV(u,v,w) = \sum_i \sum_j \sum_k N_{i,d,\tau_i}(u) N_{j,d,\tau_j}(v) N_{k,d,\tau_k}(w) \cdot C_{ijk}. - Given a target vertex
\vec{p}^*and an initial guess\vec{p}=V(u,v,w)we define the error--function for the gradient--descent as:Err(u,v,w,\vec{p}^{*}) = \vec{p}^{*} - V(u,v,w)
Implementation of FFD
- Derivation is straightforward
yielding a Jacobian:\scriptsize \begin{array}{rl} \displaystyle \frac{\partial Err_x}{\partial u} & p^{*}_x - \displaystyle \sum_i \sum_j \sum_k N_{i,d,\tau_i}(u) N_{j,d,\tau_j}(v) N_{k,d,\tau_k}(w) \cdot {c_{ijk}}_x \\ = & \displaystyle - \sum_i \sum_j \sum_k N'_{i,d,\tau_i}(u) N_{j,d,\tau_j}(v) N_{k,d,\tau_k}(w) \cdot {c_{ijk}}_x \end{array}
\scriptsize
J(Err(u,v,w)) =
\left(
\begin{array}{ccc}
\frac{\partial Err_x}{\partial u} & \frac{\partial Err_x}{\partial v} & \frac{\partial Err_x}{\partial w} \\
\frac{\partial Err_y}{\partial u} & \frac{\partial Err_y}{\partial v} & \frac{\partial Err_y}{\partial w} \\
\frac{\partial Err_z}{\partial u} & \frac{\partial Err_z}{\partial v} & \frac{\partial Err_z}{\partial w}
\end{array}
\right)
Implementation of FFD
- Armed with this we iterate the formula
J(Err(u,v,w)) \cdot \Delta \left( \begin{array}{c} u \\ v \\ w \end{array} \right) = -Err(u,v,w)using Cramer's rule for inverting the small Jacobian. - Usually terminates after
3to5iteration with an $\epsilon := \vec{p^*} - V(u,v,w) < 10^{-4}$ - self-intersecting grids can invalidate the results
- no problem, as these get not generated and contradict some properties we want (like locality)
Outline
- What is FFD?
- What is evolutionary optimization?
- How to measure evolvability?
- Scenarios
- Results
What is evolutionary optimization?
1 1
$t := 0$;
initialize $P(0) := \{\vec{a}_1(0),\dots,\vec{a}_\mu(0)\} \in I^\mu$;
evaluate $F(0) : \{\Phi(x) | x \in P(0)\}$;
while($c(F(t)) \neq$ true) {
recombine: $P’(t) := r(P(t))$;
mutate: $P''(t) := m(P’(t))$;
evaluate $F(t) : \{\Phi(x) | x \in P''(t)\}$
select: $P(t + 1) := s(P''(t) \cup Q,\Phi)$;
$t := t + 1$;
}
$t$: Iteration-step
$I$: Set of possible Individuals
$P$: Population of Individuals
$F$: Fitness of Individuals
$Q$: Either set of parents or $\emptyset$
$r(..) : I^\mu \mapsto I^\lambda$
$m(..) : I^\lambda \mapsto I^\lambda$
$s(..) : I^{\lambda + \mu} \mapsto I^\mu$
- Algorithm to model simple inheritance
- Consists of three main steps
- recombination
- mutation
- selection
- An "individual" in our case is the displacement of control-points
Evolutional loop
- Recombination generates
\lambdanew individuals based on the characteristics of the\muparents.- This makes sure that the next guess is close to the old guess.
- Mutation introduces new effects that cannot be produced by mere recombination of the
parents.
- Typically these are minor defects to individual members of the population i.e. through added noise
- Selection selects
\muindividuals from the children (and optionally the parents) using a fitness--function\Phi.- Fitness could mean low error, good improvement, etc.
- Fitness not solely determines who survives, there are many possibilities
Outline
- What is FFD?
- What is evolutionary optimization?
- How to measure evolvability?
- Scenarios
- Results
How to measure evolvability?
- Different (conflicting) optimization targets
- convergence speed?
- convergence quality?
- As
\vec{v} = \vec{U}\vec{p}is linear, we can also look at $\Delta \vec{v} = \vec{U}, \Delta \vec{p}$- We only change
\Delta \vec{p}, so evolvability should only use\vec{U}for predictions
- We only change
Evolvability criteria
- Variability
- roughly: "How many actual Degrees of Freedom exist?"
- Defined by
\mathrm{variability}(\vec{U}) := \frac{\mathrm{rank}(\vec{U})}{n} \in [0..1] - in FFD this is
1/\#\textrm{CP}for the number of control-points used for parametrization
Evolvability criteria
- Regularity
- roughly: "How numerically stable is the optimization?"
- Defined by
\mathrm{regularity}(\vec{U}) := \frac{1}{\kappa(\vec{U})} = \frac{\sigma_{min}}{\sigma_{max}} \in [0..1]with\sigma_{min/max}being the least/greatest right singular value. - high, when
\|\vec{Up}\| \propto \|\vec{p}\|
Evolvability criteria
- Improvement Potential
- roughly: "How good can the best fit become?"
- Defined by
\mathrm{potential}(\vec{U}) := 1 - \|(\vec{1} - \vec{UU}^+)\vec{G}\|^2_Fwith a unit-normed guessed gradient\vec{G}
Outline
- What is FFD?
- What is evolutionary optimization?
- How to measure evolvability?
- Scenarios
- Results
Scenarios
- 2 Testing Scenarios
- 1-dimensional fit
- $xy$-plane to $xyz$-model, where only the $z$-coordinate changes
- can be solved analytically with known global optimum
- 3-dimensional fit
- fit a parametrized sphere into a face
- cannot be solved analytically
- number of vertices differ between models
1D-Scenario
3D-Scenarios
Outline
- What is FFD?
- What is evolutionary optimization?
- How to measure evolvability?
- Scenarios
- Results
Variability 1D
- Should measure Degrees of Freedom and thus quality
5 \times 5,7 \times 7and10 \times 10have very strong correlation (-r_S = 0.94, p = 0) between the variability and the evolutionary error.
Variability 3D
- Should measure Degrees of Freedom and thus quality
4 \times 4 \times 4,5 \times 5 \times 5and6 \times 6 \times 6have very strong correlation (-r_S = 0.91, p = 0) between the variability and the evolutionary error.
Varying Variability
1 1
Regularity 1D
- Should measure convergence speed
- Not in our scenarios - maybe due to the fact that a better solution simply takes longer to converge, thus dominating.
Regularity 3D
- Should measure convergence speed
- Only very weak correlation
- Point that contributes the worst dominates regularity by lowering the least right singular value towards 0.
Improvement Potential in 1D
- Should measure expected quality given a gradient
- very strong correlation of
- r_S = 1.0, p = 0. - Even with a distorted gradient
Improvement Potential in 3D
- Should measure expected quality given a gradient
- weak to moderate correlation within each group.
Summary
- Variability and Improvement Potential are good measurements in our cases
- Regularity does not work well because of small singular right values
- But optimizing for regularity could still lead to a better grid-setup (not shown, but likely)
- Effect can be dominated by other factors (i.e. better solutions just take longer)
Outlook / Further research
- Only focused on FFD, but will DM-FFD perform better?
- for RBF the indirect manipulation also performed worse than the direct one
- Do grids with high regularity indeed perform better?
Thank you
Any questions?
![Example of Basis-Functions for degree 2. [Brunet, 2010] Note, that Brunet starts his index at -d opposed to our definition, where we start at 0.](/Drezil/masterarbeit/media/branch/master/arbeit/img/unity.png)