chemodiversity/vortrag/vortrag.md

title	subtitle	author	license	affiliation	abstract	date	papersize	fontsize	documentclass	margin	slideNumber
Chemodiversity	A short overview of this project	Stefan Dresselhaus	BSD	Theoretic Biology Group<br> Bielefeld University	Attempt to find indications for chemodiversity in the plant secondary metabolism according to the screening hypothesis	\today	a4	10pt	scrartcl	0.2	true

• It was observed, that many plants seem to produce many compounds with no obvious purpose
• Using resources to produce such compounds (instead of i.e. growing) should yield a fitness-disadvantage
• one expects evolution to eliminate such behavior

Question: Why is this behavior observed?

• Are these compounds necessary for some unresearched reason?
  • unknown environmental effects?
  • unknown intermediate products for necessary defenses?
  • speculative diversity because they could be useful after genetic mutations?

Screening Hypothesis

• First suggested by Jones & Firn (1991)
• new (random) compounds are rarely biologically active
• plants have a higher chance finding an active compound if they diversify
• many (inactive) compounds are sustained for a while because they may be precursors to biologically active substances

. . .

There are indications for and against this hypothesis by various groups.

---

Setting up a simulation

If you wish to make apple pie from scratch, you must first create the universe

• Carl Sagan

---

Defining Chemistry

• First of all we define the chemistry of our environment, so we know all possible interactions and can manipulate them at will.
• We differentiate between Substrate{.haskell} and Products{.haskell}:
  • Substrate{.haskell } can just be used (i.e. real substrates if the whole metabolism should be simulated, PPM{.haskell}^[1]^ in our simplified case)
  • Products{.haskell } are nodes in our chemistry environment.
• In Code:

  data Compound = Substrate Nutrient
                | Produced Component
                | GenericCompound Int
  

::: footer ^[1]^: plants primary metabolism :::

Usage in the current Model

• The Model used for evaluation just has one Substrate{.haskell}:
  PPM{.haskell} with a fixed Amount to account for effects of sucking primary-metabolism-products out of the primary metabolic cycle
• This is used to simulate i.e. worse growth, fertility and other things affecting the fitness of a plant.
• We are not using named Compounds, but restrict to generic Compound 1{.haskell}, Compound 2{.haskell} ...
• Not done, but worth exploring:
  • Take a "real-world" snapshot of Nutrients and Compounds and recreate them
  • See if the simulation follows the real world

Defining a Metabolism

• We define Enzyme{.haskell}s as

  • having a recipe for a chemical reaction
  • are reversible
  • may have dependencies on catalysts to be present
  • may have higher dominance over other enzymes with the same reaction

• Input can be Substrate{.haskell} and/or Products{.haskell}

• Outputs can only be Products{.haskell}

• \Rightarrow This makes them to Edges in a graph combining the chemical compounds

Usage in the current Model

• Enzyme{.haskell}s all
  • only map 1{.haskell} input to 1{.haskell} Output with a production rate of 1{.haskell} per Enzyme{.haskell}
    (i.e. -1 Compound 2 -> +1 Compound 5{.haskell})
  • are equally dominant
  • need no catalysts

Defining Predators

• Predator{.haskell}s consist of
  • a list of Compound{.haskell}s that can kill them
  • a fitness impact ([0..1]) as the probability of killing the plant
  • an expected number of attacks per generation
  • a probability ([0..1]) of appearing in a single generation
• Predator{.haskell} need not necessary be biologically motivated
  • i.e. rare, nearly devastating attacks (floods, droughts, ...) with realistic probabilities

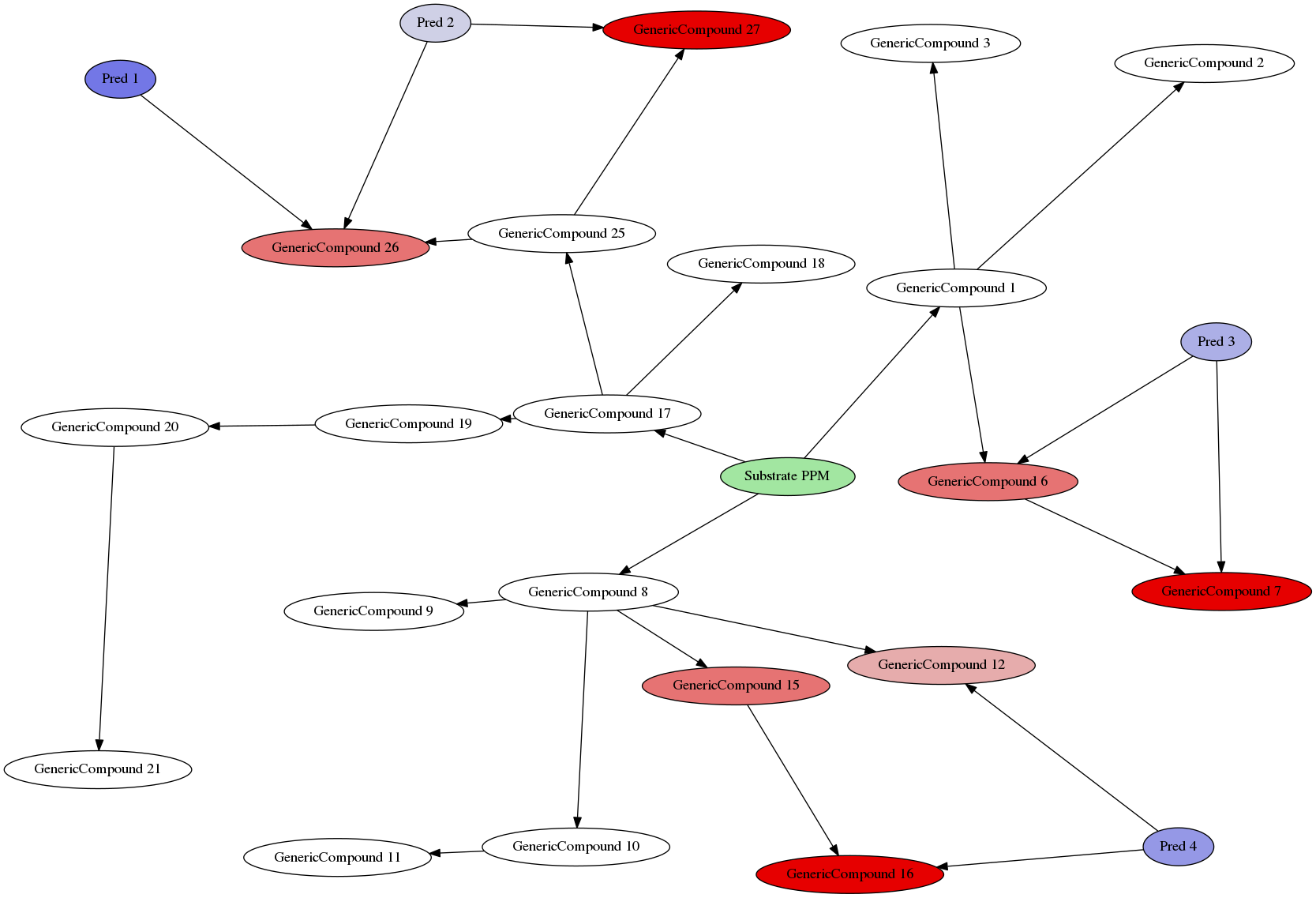
Example Environment

:::::::::::::: {.columns}

::: {.column width=37%}

• The complete environment now consists of
  • Compound{.haskell}s:
    {style="vertical-align:middle"}
  • Enzyme{.haskell}s:
    {style="vertical-align:middle"}
  • Predator{.haskell}s:
    {style="vertical-align:middle"}

:::

::: {.column width=63% .fragment}

{width=75%}

Additional rules:

• Every "subtree" from the marked PPM{.haskell} is treated as a separate species (fungi, animals, ...)
  \Rightarrow Every predator can only be affected by toxins in the same part of the tree
• Trees can be automatically generated in a decent manner to search for environmens where specific effects may arise :::

::::::::::::::

::::: notes :::::

CTRL+Click for zoom!

• All starts at PPM (Plant Primary Metabolism)
• Red = Toxic
• Blue = Predators

::::

---

Plants

A Plant{.haskell} consists of

• a Genome{.haskell}, a simple list of genes
  • Triple of (Enzyme, Quantity, Activation){.haskell}
  • without order or locality (i.e. interference of neighboring genes)
  • Quantity{.haskell} is just an optimization (=Int) to group identical Activation{.haskell}s
  • Activation{.haskell} is a float \in [0..1] to regulate the activity of the Enzyme{.haskell} genetically
• an absorbNutrients{.haskell}-Function to simulate various effects when absorbing nutrients out of the environment, depending on the environment (i.e. can use informations about chemistry, predators, etc.)
  • Not used in our simulation, as we only have PPM{.haskell} as "nutrient" and we take everything given to us.

Metabolism simulation

Creation of compounds from the given resources is an iterative process:

• First of all we create a conversion Matrix \Delta_c with corresponding startvector s_0.

• We now iterate s_i = (\mathbb{1} + \Delta_c) \cdot s_{i-1} for a fixed number of times (currently: 100) to simulate the metabolism^[2]^.

  ::: footer ::: ^[2]^: Thats a 'lie', we calculate (\mathbb{1} + \Delta_c)^{100} efficiently via lapack-internals :::

• Entries in the matrix come from the Genome{.haskell}: an Enzyme{.haskell} which converts i to j with quantity q and activity a yield

  \begin{eqnarray*}
  \Delta_c[i,j] &\mathrel{+}=& q\cdot a,\\
  \Delta_c[j,i] &\mathrel{+}=& q\cdot a, \\
  \Delta_c[i,i] &\mathrel{-}=& q\cdot a, \\
  \Delta_c[j,j] &\mathrel{-}=& q\cdot a
  \end{eqnarray*}.$$
  - This makes the Enzyme-reaction invertible as both ways get treated equally.
  
  

Metabolism-example

• Given a simple Metabolism with 1 nutrient (first row/column) and 2 Enzymes in sequence, we have given \Delta_c wtih corresponding startvector s_0:

  \Delta_c = 0.01 \cdot \begin{pmatrix}
  -1 & 1  & 0 \\
   1  & -2 & 1 \\
   0  & 1  & -1 \\
  \end{pmatrix}, s_0 = \begin{pmatrix}\text{PPM:} & 3 \\ \text{Compound1:} & 0 \\ \text{Compound2:} & 0\end{pmatrix}.$$
  
  

• In the simulation this yields us

  s_{100} \approx \begin{pmatrix}\text{PPM:} & 1 \\ \text{Compound1:} & 1 \\ \text{Compound2:} & 1\end{pmatrix},

  which is the expected outcome for an equilibrium.

Assumptions for metabolism simulation

• All Enzymes are there from the beginning
• All Enzyme-reactions are reversible without loss
• static conversion-matrix for fast calculations (unsuited, if i.e. enzymes depend on catalysts)
• One genetic enzyme corresponds to (infinitely) many real (proportional weaker) enzymes in the plant, which get controlled via the "activation" parameter

Fitness

• We handle fitness as \text{survival-probability} \in [0..1] and model each detrimental effect as probability which get multiplied together.
• To calculate the fitness of an individual we take three distinct effects into consideration:
  • Static costs of enzymes
    • Creating enzymes weakens the primary cycle and thus possibly beneficial traits (growth, attraction of beneficial organisms, ...)

      F_s := \text{static_cost_factor} \cdot \sum_i q_i \cdot a_i \quad | \quad (e_i,q_i, a_i) \in \text{Genome}

    • limits the amount of dormant enzymes
  • Cost of active enzymes
    • Cost of using up nutrients

      F_e := \text{active_cost_factor} \cdot \frac{\text{Nutrients used}}{\text{Nutrients available}}

  • Deterrence of attackers F_d (next slide)

Attacker

• Predators are modeled after Svennungsen et al. (2007)

• Each predator has an expected number of attacks P_a, that are poisson-distributed with impact P_i.

• Plants can defend themselves via

  • toxins that the predator is affected by with impact-probability D_t(P_i)
  • herd-immunity via effects like automimicry: D_{pop} = \mathbb{E}[D_t(P_i)]

• All this yields the formula:

  F_d := 1 - e^{- (D_{pop} \cdot P_a) (1-D_t(P_i))}

• The attacker-model is only valid for many reasonable assumptions

  • equilibrium population dynamics
  • equal dense population
  • which individual to attack is independently chosen
  • etc. (Details in the paper linked above)

Haploid mating

• We hold the population-size fixed at 100

• Each plant has a reproduction-probability of

  p(\textrm{reproduction}) = \frac{\textrm{plant-fitness}}{\textrm{total fitness in population}}

  yielding a fitness-weighted distribution from that 100 new offspring are drawn

• in inheritance each gene of the parent goes through different steps (with given default-values)^[3]^

  ::::: footer ^[3]^: in case of quantity q > 1 the process is repeated q times independently. ::::

  • mutation: with p_{mut} = 0.01 another random enzyme is produced, but activation kept
  • duplication: with p_{dup} = 0.05 the gene gets duplicated (quantity +1)
  • deletion: with p_{del} = p_{dup} the gene get deleted (or quantity -1)
  • addition: with p_{add} = 0.005 an additional gene producing a random enzyme with activation 0.5 gets added as mutation from genes we do not track (i.e. primary cycle)
  • activation-noise: activation is changed by c_{noise} = \pm 0.01 drawn from a uniform distribution, clamped to [0..1]

:::: notes

• Default values not motivated in any way!
• finding out how these values influence is core! ::::

---

Simulations

• Overall question: What parameters are necessary for chemodiversity?
  • How can we see chemodiversity?
  • We define an Enzyme E as divers, if the average of this Enzyme in the population stays below 0.5, so E_i \in E_{div} \text{iff.} \mathbb{E}[E_i] < 0.5
  • We can then count the number of diverse Enzymes per plant $E_{d,p_i} = |\left\lbrace E_i | E_i \in E_{div}, E_{i,p_i} > 0.5, \right\rbrace|$
• To get an insight into how this behaves we observe several other parameters every generation:
  • Fitness \in [0..1]
  • Number of different compounds created
  • Amount of compounds created
  • Number of Plants theoretically resistant to predator i (i.e. can produce a toxin to defend themselves, albeit not to 100\%.

Simulations (cont.)

• General setup of the simulation:
  • All using the example-environment shown before
    • 27 different compounds, 1 Nutrient (simulating the primary metabolism)
    • 7 of 27 compounds are toxic
    • at least 3 compounds are needed for total immunity
    • 4 predators
  • Duration of 2000 generations
• Different setups tested:
  • Behavior of predators (AlwaysAttack{.haskell}, AttackRandom{.haskell}, AttackInterval Int{.haskell})
  • varying \text{static_enzyme_cost} from 0.0 to 0.20 in steps of 0.02
    • effectively limits the amount of maximal enzymes to \frac{1}{\text{static_enzyme_cost}}
  • varying \text{nutrient_impact} from 0.0 to 1.0 in steps of 0.1
    • makes toxins less/more costly to produce

---

Results

It doesn't matter how beautiful your theory is, it doesn't matter how smart you are. If it doesn't agree with experiment, it's wrong.

• Richard P. Feynman

---

Effect of Predator-Behavior onto chemodiversity

Effect of static enzyme cost

Effect of static enzyme cost (cont.)

Effect of static enzyme cost (cont.)

Effect of nutrient-impact

Effect of nutrient-impact (cont.)

Effect of nutrient-impact (cont.)