Introduction
- Many modern industrial design processes require advanced optimization methods due to increased complexity
- Examples are
- physical domains
- aerodynamics (i.e. drag)
- fluid dynamics (i.e. throughput of liquid)
- NP-hard problems
- layouting of circuit boards
- stacking of 3D–objects
- physical domains
Motivation
- Evolutionary algorithms cope especially well with these problem domains
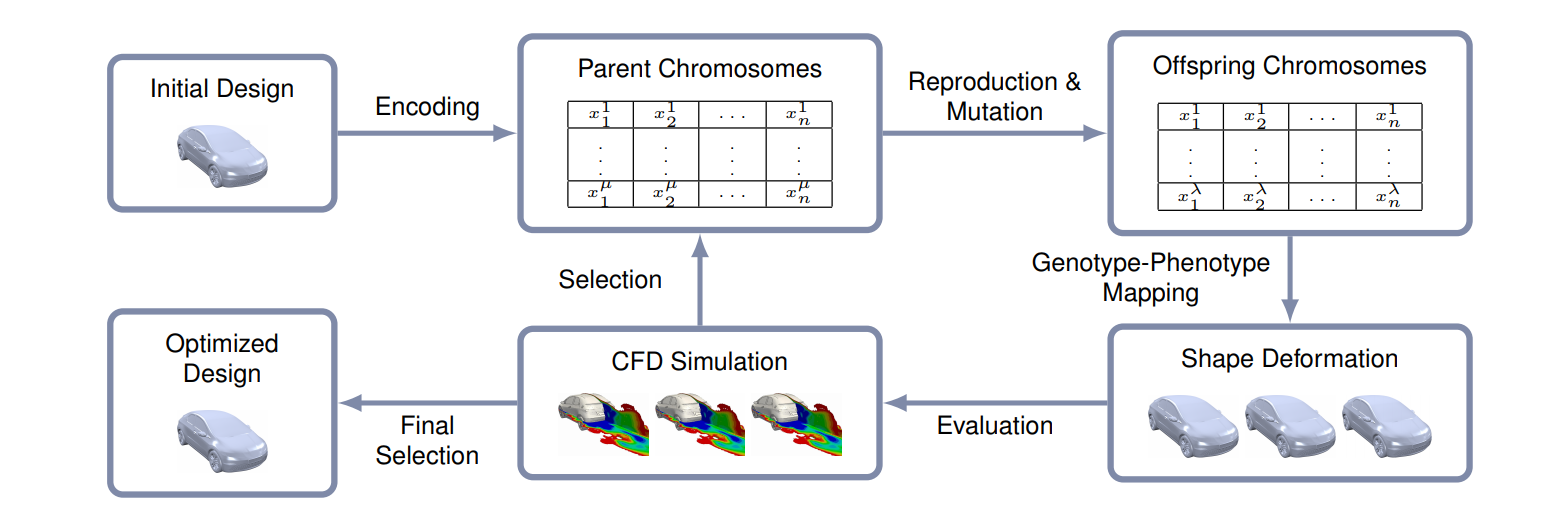
Example of the use of evolutionary algorithms in automotive design - But formulation can be tricky
Motivation
- Problems tend to be very complex
- i.e. a surface with \(n\) vertices has \(3\cdot n\) Degrees of Freedom (DoF).
- Need for a small-dimensional representation that manipulates the high-dimensional problem-space.
- We concentrate on smooth deformations (\(C^3\)-continuous)
- But what representation is good?
What representation is good?
- In biological evolution this measure is called evolvability.
- no consensus on definition
- meaning varies from context to context
- measurable?
- Measure depends on representation as well.
RBF and FFD
- Andreas Richter uses Radial Basis Functions (RBF) to smoothly deform meshes
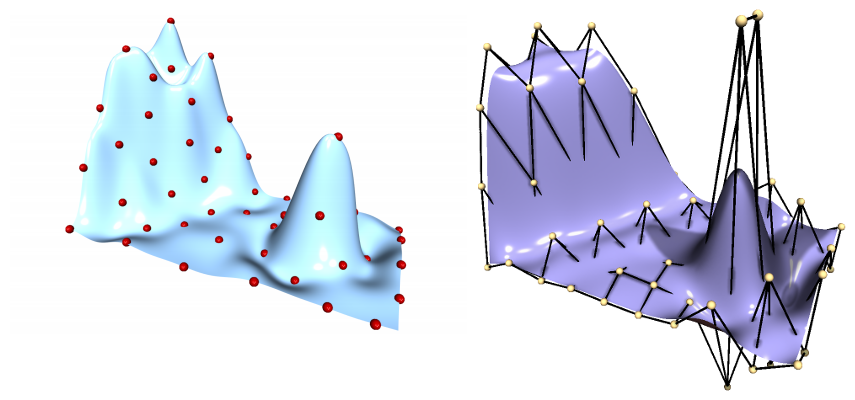
RBF and FFD
- My master thesis transferred his idea to Freeform-Deformation (FFD)
- same setup
- same measurements
- same results?

Outline
- What is FFD?
- What is evolutionary optimization?
- How to measure evolvability?
- Scenarios
- Results
What is FFD?
- Create a function \(s : [0,1[^d \mapsto \mathbb{R}^d\) that is parametrized by some special control–points \(p_i\) with coefficient functions \(a_i(u)\): \[ s(\vec{u}) = \sum_i a_i(\vec{u}) \vec{p_i} \]
- All points inside the convex hull of \(\vec{p_i}\) accessed by the right \(u \in [0,1[^d\).
Definition B-Splines
- The coefficient functions \(a_i(u)\) in \(s(\vec{u}) = \sum_i a_i(\vec{u}) \vec{p_i}\) are different for each control-point
- Given a degree \(d\) and position \(\tau_i\) for the \(i\)th control-point \(p_i\) we define \[\begin{equation} N_{i,0,\tau}(u) = \begin{cases} 1, & u \in [\tau_i, \tau_{i+1}[ \\ 0, & \mbox{otherwise} \end{cases} \end{equation}\] and \[\begin{equation} \label{eqn:ffd1d2} N_{i,d,\tau}(u) = \frac{u-\tau_i}{\tau_{i+d}} N_{i,d-1,\tau}(u) + \frac{\tau_{i+d+1} - u}{\tau_{i+d+1}-\tau_{i+1}} N_{i+1,d-1,\tau}(u) \end{equation}\]
- The derivatives of these coefficients are also easy to compute: \[\frac{\partial}{\partial u} N_{i,d,r}(u) = \frac{d}{\tau_{i+d} - \tau_i} N_{i,d-1,\tau}(u) - \frac{d}{\tau_{i+d+1} - \tau_{i+1}} N_{i+1,d-1,\tau}(u)\]
Properties of B-Splines
- Coefficients vanish after \(d\) differentiations
- Coefficients are continuous with respect to \(u\)
- A change in prototypes only deforms the mapping locally
(between \(p_i\) to \(p_{i+d+1}\))
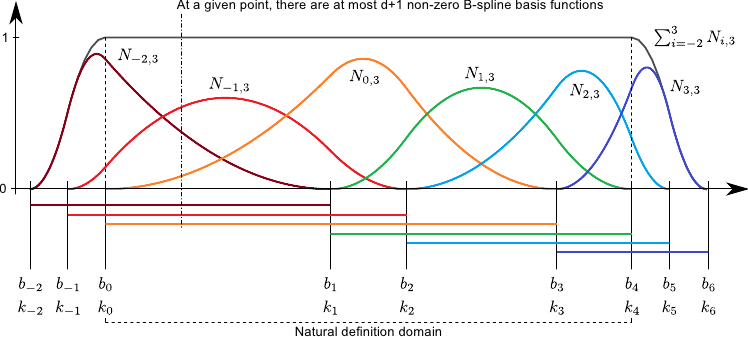
Note, that Brunet starts his index at \(-d\) opposed to our definition, where we start at \(0\).
Definition FFD
- FFD is a space-deformation resulting based on the underlying B-Splines
- Coefficients of space-mapping \(s(u) = \sum_j a_j(u) p_j\) for an initial vertex \(v_i\) are constant
- Set \(u_{i,j}~:=~N_{j,d,\tau}\) for each \(v_i\) and \(p_j\) to get the projection: \[ v_i = \sum_j u_{i,j} \cdot p_j = \vec{u}_i^{T} \vec{p} \] or written with matrices: \[ \vec{v} = \vec{U} \vec{p} \]
- \(\vec{U}\) is called deformation matrix
Implementation of FFD
- As we deal with 3D-Models we have to extend the introduced 1D-version
- We get one parameter for each dimension: \(u,v,w\) instead of \(u\)
- Task: Find correct \(u,v,w\) for each vertex in our model
- We used a gradient-descent (via the gauss-newton algorithm)
Implementation of FFD
- Given \(n,m,o\) control-points in \(x,y,z\)–direction each Point inside the convex hull is defined by \[V(u,v,w) = \sum_i \sum_j \sum_k N_{i,d,\tau_i}(u) N_{j,d,\tau_j}(v) N_{k,d,\tau_k}(w) \cdot C_{ijk}.\]
- Given a target vertex \(\vec{p}^*\) and an initial guess \(\vec{p}=V(u,v,w)\) we define the error–function for the gradient–descent as: \[Err(u,v,w,\vec{p}^{*}) = \vec{p}^{*} - V(u,v,w)\]
Implementation of FFD
- Derivation is straightforward \[ \scriptsize \begin{array}{rl} \displaystyle \frac{\partial Err_x}{\partial u} & p^{*}_x - \displaystyle \sum_i \sum_j \sum_k N_{i,d,\tau_i}(u) N_{j,d,\tau_j}(v) N_{k,d,\tau_k}(w) \cdot {c_{ijk}}_x \\ = & \displaystyle - \sum_i \sum_j \sum_k N'_{i,d,\tau_i}(u) N_{j,d,\tau_j}(v) N_{k,d,\tau_k}(w) \cdot {c_{ijk}}_x \end{array} \] yielding a Jacobian:
\[ \scriptsize J(Err(u,v,w)) = \left( \begin{array}{ccc} \frac{\partial Err_x}{\partial u} & \frac{\partial Err_x}{\partial v} & \frac{\partial Err_x}{\partial w} \\ \frac{\partial Err_y}{\partial u} & \frac{\partial Err_y}{\partial v} & \frac{\partial Err_y}{\partial w} \\ \frac{\partial Err_z}{\partial u} & \frac{\partial Err_z}{\partial v} & \frac{\partial Err_z}{\partial w} \end{array} \right) \]
Implementation of FFD
- Armed with this we iterate the formula \[J(Err(u,v,w)) \cdot \Delta \left( \begin{array}{c} u \\ v \\ w \end{array} \right) = -Err(u,v,w)\] using Cramer’s rule for inverting the small Jacobian.
- Usually terminates after \(3\) to \(5\) iteration with an \(\epsilon := \vec{p^*} - V(u,v,w) < 10^{-4}\)
- self-intersecting grids can invalidate the results
- no problem, as these get not generated and contradict some properties we want (like locality)
Outline
- What is FFD?
- What is evolutionary optimization?
- How to measure evolvability?
- Scenarios
- Results
What is evolutionary optimization?
$t := 0$;
initialize $P(0) := \{\vec{a}_1(0),\dots,\vec{a}_\mu(0)\} \in I^\mu$;
evaluate $F(0) : \{\Phi(x) | x \in P(0)\}$;
while($c(F(t)) \neq$ true) {
recombine: $P’(t) := r(P(t))$;
mutate: $P''(t) := m(P’(t))$;
evaluate $F(t) : \{\Phi(x) | x \in P''(t)\}$
select: $P(t + 1) := s(P''(t) \cup Q,\Phi)$;
$t := t + 1$;
}$t$: Iteration-step
$I$: Set of possible Individuals
$P$: Population of Individuals
$F$: Fitness of Individuals
$Q$: Either set of parents or $\emptyset$
$r(..) : I^\mu \mapsto I^\lambda$
$m(..) : I^\lambda \mapsto I^\lambda$
$s(..) : I^{\lambda + \mu} \mapsto I^\mu$- Algorithm to model simple inheritance
- Consists of three main steps
- recombination
- mutation
- selection
- An “individual” in our case is the displacement of control-points
Evolutional loop
- Recombination generates \(\lambda\) new individuals based on the characteristics of the \(\mu\) parents.
- This makes sure that the next guess is close to the old guess.
- Mutation introduces new effects that cannot be produced by mere recombination of the parents.
- Typically these are minor defects to individual members of the population i.e. through added noise
- Selection selects \(\mu\) individuals from the children (and optionally the parents) using a fitness–function \(\Phi\).
- Fitness could mean low error, good improvement, etc.
- Fitness not solely determines who survives, there are many possibilities
Outline
- What is FFD?
- What is evolutionary optimization?
- How to measure evolvability?
- Scenarios
- Results
How to measure evolvability?
- Different (conflicting) optimization targets
- convergence speed?
- convergence quality?
- As \(\vec{v} = \vec{U}\vec{p}\) is linear, we can also look at \(\Delta \vec{v} = \vec{U}\, \Delta \vec{p}\)
- We only change \(\Delta \vec{p}\), so evolvability should only use \(\vec{U}\) for predictions
Evolvability criteria
- Variability
- roughly: “How many actual Degrees of Freedom exist?”
- Defined by \[\mathrm{variability}(\vec{U}) := \frac{\mathrm{rank}(\vec{U})}{n} \in [0..1]\]
- in FFD this is \(1/\#\textrm{CP}\) for the number of control-points used for parametrization
Evolvability criteria
- Regularity
- roughly: “How numerically stable is the optimization?”
- Defined by \[\mathrm{regularity}(\vec{U}) := \frac{1}{\kappa(\vec{U})} = \frac{\sigma_{min}}{\sigma_{max}} \in [0..1]\] with \(\sigma_{min/max}\) being the least/greatest right singular value.
- high, when \(\|\vec{Up}\| \propto \|\vec{p}\|\)
Evolvability criteria
- Improvement Potential
- roughly: “How good can the best fit become?”
- Defined by \[\mathrm{potential}(\vec{U}) := 1 - \|(\vec{1} - \vec{UU}^+)\vec{G}\|^2_F\] with a unit-normed guessed gradient \(\vec{G}\)
Outline
- What is FFD?
- What is evolutionary optimization?
- How to measure evolvability?
- Scenarios
- Results
Scenarios
- 2 Testing Scenarios
- 1-dimensional fit
- \(xy\)-plane to \(xyz\)-model, where only the \(z\)-coordinate changes
- can be solved analytically with known global optimum
- 3-dimensional fit
- fit a parametrized sphere into a face
- cannot be solved analytically
- number of vertices differ between models
1D-Scenario
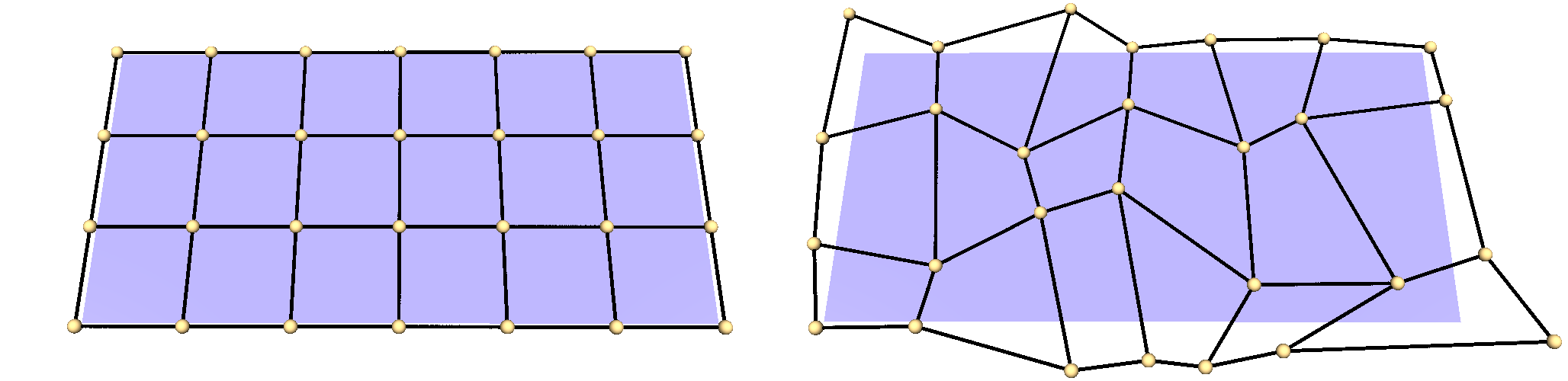
Right: The same grid after a random distortion to generate a testcase.

3D-Scenarios

Right: The face we want to deform the sphere into with 12 024 vertices.
Outline
- What is FFD?
- What is evolutionary optimization?
- How to measure evolvability?
- Scenarios
- Results
Variability 1D
- Should measure Degrees of Freedom and thus quality

Note that \(7 \times 4\) and \(4 \times 7\) have the same number of control–points.
- \(5 \times 5\), \(7 \times 7\) and \(10 \times 10\) have very strong correlation (\(-r_S = 0.94, p = 0\)) between the variability and the evolutionary error.
Variability 3D
- Should measure Degrees of Freedom and thus quality

Note that the number of control–points is a product of the resolution, so \(X \times 4 \times 4\) and \(4 \times 4 \times X\) have the same number of control–points.
- \(4 \times 4 \times 4\), \(5 \times 5 \times 5\) and \(6 \times 6 \times 6\) have very strong correlation (\(-r_S = 0.91, p = 0\)) between the variability and the evolutionary error.
Varying Variability
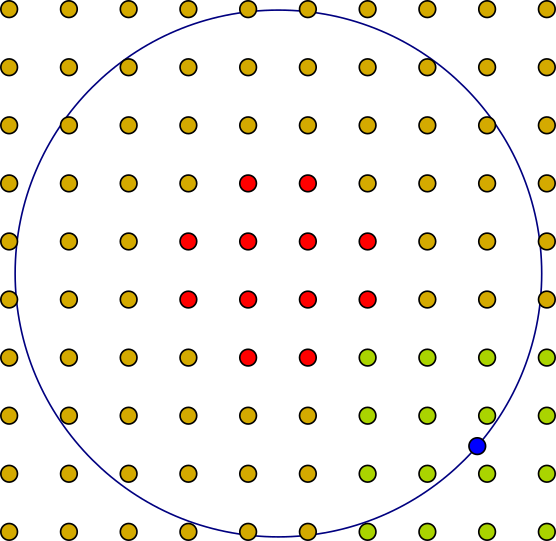
An Example–point (blue) is solely determined by the position of the green control–points.

Regularity 1D
- Should measure convergence speed

Right: Regularity against number of iterations until convergence
Coloured by their grid–resolution, both with a linear fit over the whole dataset.
- Not in our scenarios - maybe due to the fact that a better solution simply takes longer to converge, thus dominating.
Regularity 3D
- Should measure convergence speed

- Only very weak correlation
- Point that contributes the worst dominates regularity by lowering the least right singular value towards 0.
Improvement Potential in 1D
- Should measure expected quality given a gradient

- very strong correlation of \(- r_S = 1.0, p = 0\).
- Even with a distorted gradient
Improvement Potential in 3D
- Should measure expected quality given a gradient

- weak to moderate correlation within each group.
Summary
- Variability and Improvement Potential are good measurements in our cases
- Regularity does not work well because of small singular right values
- But optimizing for regularity could still lead to a better grid-setup (not shown, but likely)
- Effect can be dominated by other factors (i.e. better solutions just take longer)
Outlook / Further research
- Only focused on FFD, but will DM-FFD perform better?
- for RBF the indirect manipulation also performed worse than the direct one
- Do grids with high regularity indeed perform better?
Thank you
Any questions?